Proofs, Arguments, and Zero-Knowledge

Author:#JustinThaler Version: July 18, 2023 ProofsArgsAndZK_annotated.pdf

Chapter 1: Introduction

• Definitions:
  • Verifiable Computing (VC) and Interactive Proofs (IP): enable a prover to provide a guarantee to a verifier that the prover performed a requested computation correctly
  • Arguments of Knowledge: Allows for false proofs if they require exorbitant computational power to find
  • Zero Knowledge: Proof reveals nothing but the validity of the statement

Chapter 2: The Power of Randomness: Fingerprinting and Freivalds’ Algorithm

• Reed-Solomon Fingerprinting:
  • Setting: Alice and Bob want to check whether they have the same file
  • Protocol: Both parties compute a fingerprint and check whether it is the identical
  • Reed-Solomon Encoding: For some prime $p<n^2$, interpret the file as messages in ${\mathbb{F}}_p^n$ and consider the family of hash functions: $h_r(a_1,...,a_n)={\sum }_{i=1}^n{a}_i\cdot r^{i-1}$ for $r\in {\mathbb{F}}_p$
  • → Collision resistant because to unequal polynomials of degree $d$ can only agree on $d$ points
• Freivald’s algorithm:
  • Setting: Given two matrices $A$ and $B$ of size $n^2$, compute $C=AB$. The fastest known algorithm is $O(n^{2.37286})$, but it is possible to verify that $C$ is computed correctly in time $O(n^2)$
  • Let $x=(1,r,r^2,...,r^{n-1})$, compute $y=Cx$ and $z=A\cdot Bx$, accept if they are equal
  • → Each entry in the the vectors are Reed-Solomon fingerprints of a row of $C$ and $(AB)$, respectively
• Univariate Lagrange interpolation: See Low Degree and Multilinear Extensions
• Evaluating $q_a(r)$: All values ${\delta }_j(r)$ can be evaluated in $O(n)$ operations in total, by starting with ${\delta }_0(r)$ and computing ${\delta }_i(r)$ from ${\delta }_{i-1}(r)$ (which has almost the same terms) in constant time
  • → Total time to evaluate is $O(n)$

Chapter 3: Definitions and Technical Preliminaries

• Interactive Proof System (IP):
  • Probabilistic verifier and deterministic prover which are “next-message passing algorithms”
  • Both parties are given $x\in \{0,1{\}}^n$; at the beginning, the prover provides a value claimed to equal $f(x)$
  • $t:=(m_1,m_2,...,m_k)$ is called the transcript
  • $out(V,x,r,P)\in \{0,1\}$ is the deterministic output of $V$ given its randomness $r$, input $x$ and prover strategy $P$
  • An IP is valid if it is sound and complete
• Argument systems: An IP for which soundness is only required to hold against prover strategies that run in polynomial time
• Schwartz-Zippel Lemma
• Low Degree and Multilinear Extensions

Chapter 4: Interactive Proofs

• Multivariate Sum-Check Protocol
• Application of the Sum-Check protocol to#SAT:
  • Boolean formula: A boolean circuit with fan-out of 1 for all non-output gates
  • Goal: Given a boolean formula $\varphi$, compute ${\sum }_{x\in \{0,1{\}}^n}\varphi (x)$, i.e., the number of inputs for which $\varphi$ outputs $1$
  • → Fastest known algorithm needs exponential time!
  • Approach: Turn $\varphi$ into an arithmetic circuit over $\mathbb{F}$ by replacing $AND(x,y)$ gates by $x\cdot y$, $OR(x,y)$ by $x+y-x\cdot y$, etc.; then apply the sum-check protocol to this multivariate polynomial
• A simple IP for Counting Triangles in Graphs:
  • Given an adjacency matrix $A$ for a given graph, the number of triangles can be computed as $\Delta =\frac{1}{6}sum(A^3)$
  • For any given $A$, there is a function $f_A:\{0,1{\}}^{\log n}\times \{0,1{\}}^{\log n}\to \{0,1\}$ that takes the binary representations of row and column indices and outputs the entry of the matrix at that position
  • Therefore, $\Delta =\frac{1}{6}{\sum }_{x,y,z\in \{0,1{\}}^{\log n}}{f}_A(x,y)\cdot f_A(y,z)\cdot f_A(x,z)$
  • → Can apply the sum-check protocol to $g(X,Y,Z)=\widetilde{f_A}(X,Y)\cdot \widetilde{f_A}(Y,Z)\cdot \widetilde{f_A}(X,Z)$
• Reducing Multiple Evaluations to One
• Super-Efficient IP for Matrix Multiplication
• GKR

Chapter 5: Publicly Verifiable, Non-interactive Arguments via Fiat-Shamir

• Random Oracle Model (ROM): Prover and verifier have access to some random function
  • Does not exist in practice: A random function would have to be represented by a function table which would be huge for cryptographic security levels
  • In practice, no deployed system has been broken because of this
• Fiat-Shamir Transformation: Verifier message in round $i$ is the evaluation of a cryptographic hash function quere the query point is the list of messages sent by the prover in rounds $1,...,i$
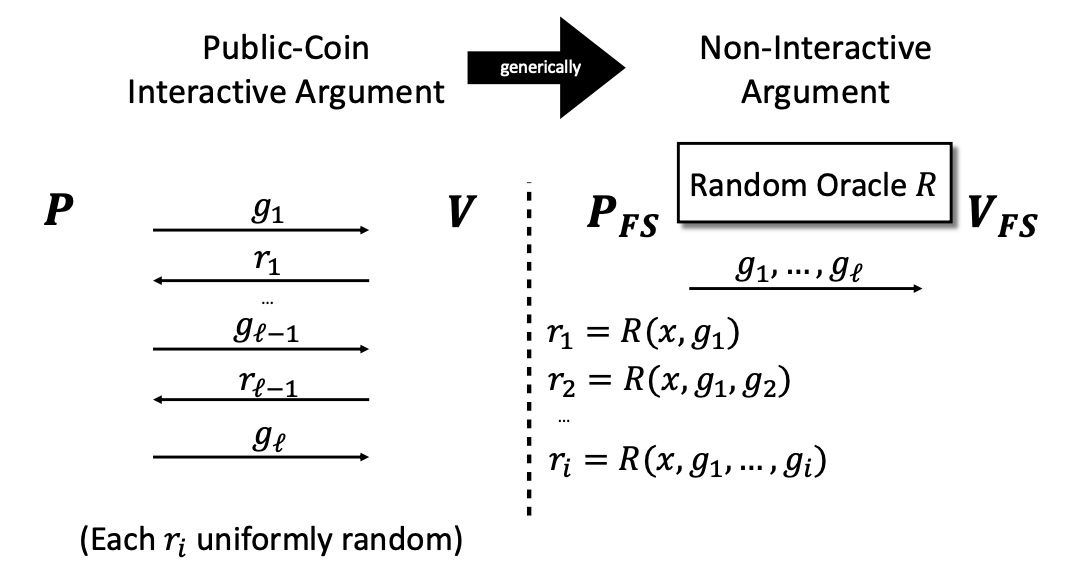
  • Secure in the ROM on constant-round public coin IPs where the prover has to run in polynomial time
  • Hash chaining: To save on the cost of hashing, one can also use $r_i:=h(x,i,r_{i-1},g_i)$
  • If the prover can choose $x$ (e.g. the input to the circuit proved by the GKR protocol) freely, it is essential that $x$ is part of the transcript
• Correlation-intractability (CI): A hash family satisfies CI on some property if it is computationally infeasible to find a pair $(y,h(y)$ that satisfies the property
  • There are hash families for various classes of IPs & arguments, with the CI property holding under standard cryptographic assumptions, but they are very expensive and hence impractical

Chapter 6: Front Ends: Turning Computer Programs Into Circuits

• Front end: Program -to-circuit compiler
• Back end: The argument system
• Goal: turn arbitrary programs running on a Random Access Machine (RAM) (memory + registers + instructions + PC) in $T$ steps into arithmetic circuits
• Preliminary techniques:
  • Evaluate step-by-step: In each layer, list the entire machine configuration (e.g. representing each memory cell as 64 binary field elements) and repeatedly apply a sub-circuit that performs one computations step
    • Unusable in the context of GKR, because the number of layers (and hence verifier time) is $\Theta (T)$
    • Massive circuit, because each memory cell is repeated in each step
  • Turning small-space programs into shallow circuits: If the program uses little space the configuration graph is small and can be represented using an adjacency matrix. Running the machine for $n$ steps is equivalent to squaring the matrix $\log n$ times.
• Circuit satisfiability problem: There exists a witness $w$ such that $C(x,w)=y$
  • This is in contrast to the circuit evaluation problem where we show that $C(x)=y$
• Transcript or trace: The list of changes to the machine configuration in each time step, of size $O(T)$
  • If a memory operation happened, contains a memory location & value
• Transformation from computer programs to arithmetic circuit satisfiability: The circuit takes the transcript as witness and checks two properties:
  • Memory consistency: When a value is read, it needs to return the most recently written value to that location
  • Time consistency: Assuming memory consistency holds, check that the transition from step $i$ to $i+1$ was correct
• Checking for time consistency:
  • Can be done in parallel!
  • Example: Implementing $a>b$ ($a,b\in {\mathbb{F}}_p$, $l:=\lceil \log p\rceil$)
    • Add $2l$ witness values $a_0,...,a_{l-1},b_0,...,b_{l-1}$ representing the bit representations of $a$ and $b$
    • Add output gates that compute $a_i^2-a_i$ → 0 iff. all $a_i$ are binary
    • Add output gate that computes $a-{\sum }_{i=0}^l{a}_i{2}^i$ → 0 iff. binary decomposition is correct
      • Error: I don’t think that’s sound, the sum could overflow the field
    • For $j=l-2,l-3,...,1$, define:
      • $A_j:={\prod }_{j^{\prime }>j}(a_{j^{\prime }}{b}_{j^{\prime }}+(1-a_{j^{\prime }})(1-b_{j^{\prime }}))$
        • → $1$ iff. the $l-j$ most significant bits are equal
    • The following expression equal $1$ iff. $a>b$: $a_{l-1}(1-b_{l-1}+A_{l-2}{a}_{l-2}(1-b_{l-2})+...+A_0{a}_0(1-b_0)$
• Checking for memory consistency:
  • Idea: Sort memory accesses by (address, time), then consistency can be checked by putting constraints on neighboring items
  • Routing Networks: A graph of depth $O(\log T)$ that allows the prover to permute the memory accesses in any order, using additional witness values
  • Optimizations if we allow for witnesses to false statements, but that are hard to find:
    • Memory Consistency via Merkle Trees: Every read is followed by a Merkle proof, which is validated by the circuit
      • → Lots of hashes, but efficient if there are few memory operations
    • Adapt Offline Memory Checking
• Efficiently representing non-arithmetic operations over large prime-order fields:
  • Bootle et al. (2018, Arya):
    • Instead of bit-decomposing elements, use base $b=2^{W/c}$ where $W$ is the word size and $c$ is a constant
    • The range-check happens via the following lookup argument:
      • To show: values $\{f_1,...,f_N\}$ are all contained in $\{s_1,...,s_B\}$
      • → There are non-negative integers $e_1,...,e_B$ such that the following polynomials are equal: $h(X):={\prod }_{i=1}^N(X-f_i)$ and $q(X):={\prod }_{i=1}^B(X-s_i{)}^{e_i}$
      • The witness contains the bit representations of each $e_i\in \{0,1{\}}^{{\log }_{2}N}$, and an arithmetic circuit of $O(B\log N)$ gates computes for a challenge point $r$: ${\prod }_{i=1}^B{\prod }_{j=1}^{{\log }_{2}N}(r-s_i{)}^{2^j\cdot e_{i,j}}$
  • Gabizon & Williamson (2020, Plookup):
    • Simplified variant due to Cairo: All elements appear at least once and the lookup table covers a contiguous interval
    • Witness sequence $\{w_1,...,w_n\}$ is claimed to equal $\{f_1,...,f_N\}$ in sorted order
    • To show:
      • $\{w_1,...,w_n\}$ is a permutation of $\{f_1,...,f_N\}$
        • → Permutation Check via Product Check
      • $s1=w_1\le w_2\le ...\le w_N=s_B$
        • Circuit checks $s1=w_1$, $w_N=s_B$, and for each $i=2,...,N$: $(w_i-w_{i-1})\cdot (w_i-(w_{i-1}+1))=0$

Chapter 7: A First Succinct Argument for Circuit Satisfiability, from Interactive Proofs

• Idea: Instead of sending the witness to the verifier (which might be $\Theta (T)$), use a polynomial commitment scheme (PCS) to commit to $\tilde{w}$
  • If $z$ is the concatenation of $x$ and $w$ (both of the same length, a power of $2$), it’s multilinear extension is: $\tilde{z}(r_0,...,r_{\log n})=(1-r_0)\cdot \tilde{x}(r_1,...,r_{\log n})+r_0\cdot \tilde{w}(r_1,...,r_{\log n})$
• A First (Relaxed) Polynomial Commitment Scheme:
  • Build a Merkle tree of all ${\mathbb{F}}^{\log n}$ evaluations of the polynomial
    • Impractical, but included for didactic reasons
  • Then, we have to run a low-degree test to make sure that the evaluations are close to those of a low-degree polynomial
  • Example: point-versus-line test
    • Request evaluations of a random line in ${\mathbb{F}}^m$ and make sure that it corresponds to a univariate polynomial of degree at most $m$
    • Repeat a few times to reduce the soundness error
• Knowledge Soundness: Establishes not only that there exists a satisfying witness, but that the prover knows it
  • Formally shown by proving the existence of an efficient extractor: A program that can repeatedly interact with the prover to extract a valid witness
  • Why efficient? Because if it is efficient, the prover could run it by simulating the interaction with itself to compute the witness, so we can assume (s)he knows it!
  • Knowledge Soundness is a stronger property than binding

Chapter 8: MIPs and Succinct Arguments

• Multi-prover interactive proof: Instead of one prover, we have multiple, which are not allowed to communicate after the start of the protocol (otherwise, they could be simulated with just one prover)
  • In practice, they only use the second prover to model a PCS!
• Example: Run GKR, but with a PCS answering the final query on the multilinear extension of the witness!
• Spartan

Chapter 9: PCPs and Succinct Arguments

• Probabilistically Checkable Proof (PCP): The verifier has oracle access to a static proof of length $l$, where typically the verifier would query random parts of the proof
• Closely related to MIPs: Can be converted in both directions, but with considerable constant overhead
• Can be compiled to a succinct argument by having the prover commit to the proof (e.g. via a Merkle tree) and then answer the verifier queries
• A First Polynomial Length PCP, From an MIP: Basically Clover (see Spartan), but using a base larger than $2$ (to reduce variables), with the proof consisting of every possible query by the verifier → Proof size is at least $O(S^3)$
• A PCP of Quasilinear Length for Arithmetic Circuit Satisfiability: Skipped

Chapter 10: Interactive Oracle Proofs

• Interactive Oracle Proof (IOP): An IP where each round is given query access to each prover “special” message → Generalization of IP and PCP
• Polynomial IOP: Special messages specify polynomials, the verifier can query evaluations
• A polynomial IOP for R1CS-SAT via univariate sum-check:
  • Setting: To show that $(Az)\circ (Bz)=Cz$, let $z_A=Az$, $z_B=Bz$, and $z_C=Cz$, and ${\hat{z}}_A$, ${\hat{z}}_B$, and ${\hat{z}}_C$ be their unique univariate extensions over a multiplicative subgroup $H\subseteq \mathbb{F}$ and show:
    • For all $h\in H$, ${\hat{z}}_A(h)\cdot {\hat{z}}_B(h)={\hat{z}}_C(h)$
      • Run the Univariate Zero-Check Protocol on ${\hat{z}}_A(h)\cdot {\hat{z}}_B(h)-{\hat{z}}_C(h)$
    • For all $h\in H$ and $M\in \{A,B,C\}$, ${\hat{z}}_M(h)={\sum }_{j\in H}{M}_{h,j}\cdot \hat{z}(j)$
      • Let $\hat{M}:H\times H\to \mathbb{F}$ denote the bivariate low-degree extension of $M$
      • Because ${\hat{z}}_M$ is the unique extension, the following equality holds: ${\hat{z}}_M(X)={\sum }_{j\in H}\hat{M}(X,j)\hat{z}(j)$
      • The verifier checks this equality at a random point $r^{\prime }$ by executing the Univariate Zero-Check Protocol asserting that ${\sum }_{j\in H}q(j)=0$ for $q(Y):=\hat{M}(r^{\prime },Y)\hat{z}(Y)-{\hat{z}}_M(r^{\prime })\cdot |H{|}^{-1}$
      • As part of the protocol, the verifier has to evaluate $q(r^{\prime \prime })$, which involves evaluating $\hat{M}(r^{\prime },r^{\prime \prime })$
      • This can be done by having a trusted party commit to $\hat{M}$ during pre-processing using a holographic commitment scheme, which means that the prover can reveal $\hat{M}(r^{\prime },r^{\prime \prime })$ in a time that’s linear in the number of non-zero entries $k$ of $M$. Page 152 gives a holographic commitment scheme that involves committing to 3 univariate polynomials of degree $k$ (row, column, and value).
    • *Question: Does the prover really have to commit to and send the polynomials ${\hat{z}}_M$? Can’t it work like in Spartan where the prover sends ${\hat{z}}_M(r^{\prime })$ on demand which is then verified via the sum check?
• FRI
• From univariate to multilinear polynomials:
  • A multilinear polynomial is fully specified by its evaluations on the boolean hypercube, so we interpolate a univariate polynomial $Q$ that maps each element in $H$ to an evaluation at one of the hypercube points
  • To reveal $q(z)=v$, let $u_2$ be the polynomial that encodes the evaluation of all Lagrange basis polynomials at $z$
  • Then, it suffices to show that ${\sum }_{a\in H}Q(a)\cdot u_2(a)=v$
  • → Univariate Sum-Check Protocol
  • At the end of the protocol, the verifier has to evaluate $u_2(r)$ for a random point $r\in \mathbb{F}$. This is only possible in linear time.
  • However, there is a layered circuit of size $O(n\log n)$ and depth $O(\log n)$, so GKR can be used to outsource the work to the prover
• Ligero and Brakedown Polynomial Commitments

Chapter 11: Zero-Knowledge Proofs and Arguments

• Zero Knowledge: There exists a polynomial-time simulator algorithm that produces transcripts indistinguishable from those of a real interaction between a verifier & an honest prover
  • Perfect zero-knowledge: The distributions are identical
  • Statistical zero-knowledge: Negligible statistical distance
  • Computational zero-knowledge: No polynomial-time algorithm can distinguish the transcripts
  • Honest verifier zero-knowledge: Only real interactions with an honest count
• Why does the existence of a simulator not mean that the system is broken?
  • In fact, the simulator might even produce transcripts that “prove” false statements!
  • But: In a real proof, there is interaction. The simulator can already “know” later verifier messages when generating early prover messages.
• I skipped the rest of the chapter!

Chapter 12: $\Sigma$-Protocols and Commitments from Hardness of Discrete Logarithm

• Cryptographic background:
  • Group: A set + an operation that behaves much like multiplication, i.e.:
    • Closure: $a,b\in \mathbb{G}⟹a\cdot b\in \mathbb{G}$
    • Associativity: $a\cdot (b\cdot c)=(a\cdot b)\cdot c$
    • Identity: There is an element $1_{\mathbb{G}}$ s.t. $1_{\mathbb{G}}\cdot g=g\cdot 1_{\mathbb{G}}=g$
    • Invertibility: For every $g\in \mathbb{G}$ there is a $h\in \mathbb{G}$ s.t. $g\cdot h=1_{\mathbb{G}}$
    • Commutativity? (for abelian groups): $a\cdot b=b\cdot a$
  • The order of a subgroup always divides the order of the original group
  • Any prime-order subgroup is cyclic and any non-identity member is a generator
  • Other concepts not summarized here: Discrete log problem, elliptic curve groups
• Schnorr’s Σ-Protocol for knowledge of discrete logarithm
• Pedersen Commitment

Chapter 13: Zero-Knowledge via Commit-And-Prove and Masking Polynomials

• Commit-and-prove:
  • Setting: Let $C$ be an arithmetic circuit and let the prover make the claim that (s)he knows $w$ such that $C(w)=1$
  • The prover sends a Pedersen commitment for each entry of $w$ and the output of each multiplication gate
  • Then, the prover proves knowledge of an opening to these comments
  • The verifier can on its own derive commitments to outputs of addition gates
  • For multiplication gates, the prover proves a product relationship between the committed values
• zk-Arguments form IPs:
  • Again, the prover sends Pedersen commitments to entires in $w$
  • Then, GKR is executed, but with the prover messages replaced with commitments
  • → The verifier checks can be replaced with a commit-and-prove protocol using a circuit of size $O(d\log |C|+|w|)$
• Zero-knowledge via masking polynomials:
  • A zero-knowledge sum-check protocol:
    • Goal: Make the sum-check protocol applied to a polynomial $g$ zero-knowledge
    • Let the prover commit to a random multi-linear polynomial $p$
    • Let the prover send $P$ claimed to equal ${\sum }_{x\in \{0,1{\}}^l}p(x)$
    • Let the verifier choose a random challenge $\rho$
    • → Run the sum-check protocol on $g+\rho \cdot p$ (a random polynomial)
    • At the end of the protocol, the verifier queries $g(r)$
      • So, at this point, it’s not perfectly zero-knowledge!
  • Mask $g(r)$: Replace $Z=\tilde{W}$ with a slighly higher-degree extension of $W$
    1. Insist that the verifier challenges are from $\mathbb{F}\setminus \{0,1\}$
    2. The prover picks $c_1$ and $c_2$ at random and choses: $Z(X_1,\dots ,X_{\log s}):=\tilde{W}(X_1,\dots ,X_{\log s})+c_1{X}_1(1-X_1)+c_2{X}_2(1-X_2)$
    3. Insist that the commitment scheme is zero-knowledge
    4. Apply the zk-variant of the sum-check protocol

Chapter 14: Polynomial Commitments from Hardness of Discrete Logarithm

• Polynomial commitment: Allows a prover to commit to a polynomial and then later reveal the evaluation at points chosen by the verifier
  • Because the commitment is usually smaller than the polynomial, it can only be computationally binding
  • Evaluations proof can be shorter than evaluating the actual polynomial
  • They can be zero-knowledge, i.e., the verifier learns nothing about the polynomial except the evaluations
  • Often, polynomial commitment schemes are more general: They commit to a vector $u$ (e.g. the coefficients of the polynomial) and the prover to make a claim about $⟨c,u⟩$ for some known vector $u$ (e.g. $y:=(1,z,z^2,...,z^{n-1})$)
• Linear-size Pedersen Polynomial Commitment
• Generalized Pedersen Commitment
• Hyrax
• Bulletproofs

Chapter 15: Polynomial Commitments from Pairings

• Cryptographic Background:
  • Decisional Diffie-Hellman Assumption (DDH): Given a group, it is no feasible to distinguish $(g,g^a,g^b,g^{ab})$ and $(g,g^a,g^b,g^c)$, where $a,b,c$ are chosen randomly
    • → Stronger than discrete log or computational Diffie-Helman (CDH, infeasible to compute $g^{ab}$ from $g^a$ and $g^b$)
  • Bilinear map: A map $e:{\mathbb{G}}_1\times {\mathbb{G}}_2\to {\mathbb{G}}_T$ such that $w(u^a,v^b)=e(u,v{)}^{a,b}$ (where ${\mathbb{G}}_T$ is called the target group)
    • ${\mathbb{G}}_1={\mathbb{G}}_2$ implies that DDH is false!
    • In practice, if $\mathbb{G}$ is an elliptic curve group defined over ${\mathbb{F}}_p$ then ${\mathbb{G}}_T$ is a subgroup of ${\mathbb{F}}_{p^k}$ where $k$ is called the embedding degree and equal to the smallest integer such that $|\mathbb{G}|$ divides $p^k-1$
    • → Embedding degree must be low for a curve to be pairing friendly
• KZG
• Dory

Chapter 16: Wrap-Up of Polynomial Commitments

• Batch evaluation of homomorphically committed polynomials:
  • Suppose a verifier wants to know both vaues $y_1=p(r)$ and $y_2=q(r)$
  • Instead of opening both commitments individually, the verifier can pick a random challenge $a$, compute the commitment to $a\cdot p+q$ and ask the prover to open this commitment at point $r$ to value $a\cdot y_1+y_2$
• Commitment scheme for sparse Polynomials (sketch): A commitment scheme for sparse multilinear polynomials, using any commitment scheme for dense multilinear polynomials (proposed by Setty (2020))
  • Idea: Design a layered arithmetic circuit that takes a description $s$ of the $M$-sparse polynomial $q$ and $z\in {\mathbb{F}}^l$ and computes $q(z)$
  • The description $s$ is the list of:
    • $M$ coefficients
    • For each coefficient $c_i$, the bits $T_i\in \{0,1{\}}^l$ of the Lagrange basis polynomial ${\chi }_{T_i}={\prod }_{j=1}^l(T_{i,j}{X}_j+(1-T_{i,j})(1-X_j))$
  • → $O(Ml)$ gates, apply GKR
  • → To reduce to $O(l)$, specify basis polynomials via a triple of integers and use a Random Access Machine (Chapter 6) to evaluate
• Commitment schemes summary:

Chapter 17: Linear PCPs and Succinct Arguments

• Idea: Super-polynomial PCPs are fine, if the prover does not have to materialize them
• Linear PCP: The proof is interpreted as a function $\pi :{\mathbb{F}}^v\to \mathbb{F}$ for some integer $v$ (e.g. the circuit size $|S|$). The honest proof is the evaluation table of a linear function, i.e., $\pi (d_1{q}_1+d_2{q}_2)=d_1\pi (q_1)+d_2\pi (q_2)$. Equivalently, $\pi$ is a $v$-variate polynomial of total degree $1$ with a constant term of $0$.
  • That means that just to specify a query point to the polynomial, the verifier has to specify $v$ field elements!
• Commitment to a Linear function
• A first linear PCP for arithmetic circuit satisfiability: Skipped, PCP has size ${\mathbb{F}}^{S+S^2}$
• GGPR

Chapter 18: SNARK Composition and Recursion

• Idea: We can compose SNARKs, i.e., first compute a proof of the inner SNARK (e.g. one with fast prover time, not necessarily zero-knowledge) and then compute an outer SNARK (e.g. one with low proof size / verification time, possibly zero-knowledge) that only claims to have validated the inner SNARK correctly
  • When composing a SNARK with itself repeatedly, one will eventually hit the recursion threshold, where the circuit size of the validating circuit does not decrease anymore.
  • Note that the knowledge extractor runtime grows exponentially with the recursion depth. So, for super-constant recursion depth, we don’t know how to prove knowledge soundness!
• Cycle of Curves: In order to efficiently validate a SNARK using an elliptic curve group, we need a second curve whose scalar field is equal to the original curve’s base field. With a cycle of curves (e.g. the Pasta curves), we can recurse infinitely.
• Applications:
  • Incremental computation: e.g. Verifiable delay functions
  • Incrementally Verifiable Computation (IVC)
  • Proof aggregation
• Nova