Circle STARKs - notes from a seminar in Stateless Consensus EF

Author: Matan Prasma PDF: can be found here Content is also from online lectures

Naive Set Theory (Elliptic Curve Script)

• Ordered pair: $(a,b):=\{\{a\},\{a,b\}\}$
• Cartesian product: $A\times B:=\{(a,b)|a\in A,b\in B\}$
• Function: A function $f:A\to B$ is a subset $f\subset A\times B$ s.t.:
  • $\forall a\in A:\exists b\in B:(a,b)\in f$
  • $\forall (a,b)\in f,(a,b^{\prime })\in f:b=b^{\prime }$
  • ⇒ $A$ is the domain, $B$ is the range
• Function composition: $(g\circ f)(a):=g(f(a))$
• Function properties:
  • Injective, Monomorphism, “one-to-one”: $\forall x,x^{\prime }:f(x)=f(x^{\prime })⟹x=x^{\prime }$
  • Surjective, Epimorphism, “onto”: $\forall y:\exists x:f(x)=y$
  • Bijective, Isomorphism, “invertible”: Injective + Surjective
  • ⇒ Each of these properties still hold for $(g\circ f)$ if they do for $f$ and $g$
• Equivalence relations: A relation $R$ on $X$ is a subset $R\subset X\times X$
  • $x{\sim }_{R}y$ means that \mathbb{Z}_b$(x,y)\in R$
  • An equivalence relation is a relation with the properties:
    • Reflexivity: $\forall x\in X:x\sim x$
    • Symmetry: $\forall x,y\in X:x\sim y⟺y\sim x$
    • Transitivity: $\forall x,y,z\in X:x\sim y\wedge y\sim z⟹x\sim z$
  • Equivalence class: $[x]:=\{y\in X|x\sim y\}$
  • Quotient set: $X/\sim :=\{[x]|x\in X\}$
    • The quotient map maps an element $x$ to its equivalence class $[x]$
  • Example: Projective Line:
    • On some field $\mathbb{F}$, define the punctured plane as ${\mathbb{F}}^2\setminus \{(0,0)\}$
    • Equivalence relation: $(x,y)\sim (x^{\prime },y^{\prime })⟺\exists \lambda \ne 0:(x,y)=(\lambda x^{\prime },\lambda y^{\prime })$
    • The quotient set is the projective line and denoted ${\mathbb{P}}_{\mathbb{F}}^1$
    • Elements of this set are denoted as $[x:y]$
    • The number of elements is $|\mathbb{F}|+1$: One element for each possible slope, plus the “point at infinity” ($[0:1]$)

Elementary Number Theory

• Bezout’s lemma: For any positive integers $a,b$, there exist $u,v\in \mathbb{Z}$ such that: $au+bv=gcd(a,b)$
  • ⇒ These numbers can be found using the Extended Euclidean Algroithm
  • ⇒ One application: If $a<b$ and $b$ is prime, we have $gcd(a,b)=1$, so $u$ is the multiplicative inverse of $a$ in ${\mathbb{Z}}_b$
• Chinese Remainder Theorem:
  • Let $n_1,\dots ,n_k\in \mathbb{N}$ be such that $\forall i\ne j:\gcd (n_i,n_j)=1$ and denote $N=n_1\cdot \cdots \cdot n_k$.
  • Then for all $a_1,\dots ,a_k\in \mathbb{N}$, the system of equations$\begin{array}{rl}x& =a_1(\mathrm{mod}{n}_1)\\ & ⋮\\ x& =a_k(\mathrm{mod}{n}_k)\end{array}$has a unique solution in ${\mathbb{Z}}_N$.

Groups

• Group: A group consists of a set $G$, containing a neutral element $e$, and a group operation $\mu$ under the following conditions:
  • Unitary: $\forall x\in G:\mu (x,e)=\mu (e,x)=x$
  • Associativity: $\forall x,y,z\in G:\mu (\mu (x,y),z)=\mu (x,\mu (y,z))$
  • Invertibility: $\forall x\in G:\exists x^{-1}\in G:\mu (x^{-1},x)=\mu (x,x^{-1})=e$
• Common notation:
  • Additive: $e$ is denoted as $0$; $\mu$ is denoted as $+$
  • Multiplicative: $e$ is denoted as $1$; $\mu$ is denoted as $\cdot$
• Fermat’s little theorem: If $p$ is prime, $\forall a\in \{1,...,p-1\}:a^{p-1}=1\mathrm{mod}p$
• ⇒ This implies that ${\mathbb{F}}_p^{\times }=\mathbb{F}\setminus \{0\}=\{1,...,p-1\}$ is a group with multiplication modulo $p$
• Subgroup: If a for subset $H\subseteq G$ $(H,\mu ,e)$ is a group, it is called a subgroup of $G$ (denoted $H\le G$)
• Coset: Given a subgroup $H$ and an element $x\in G$, the (left) $H$-coset is defined as: $xH:=\{xh|x\in H\}$
  • $xH=yH⟺x^{-1}y\in H$
  • The set of cosets $\{xH{\}}_{x\in G}$ forms a partition of $G$
• Lagrange’s Theorem: For a finite group $G$ and subgroup $H\le G$, $\#H$ divides $\#G$
  • (Because each coset has $\#H$ elements and the set of cosets is a partition of $G$)
• Group Homomorphism: For two groups $G$ and $H$, a function $f:G\to H$ is called a group homomorphism if for any $x,y\in G$, $f(xy)=f(x)\cdot f(y)$
  • The kernel $ker(f)$ is defined as $\{x\in G|f(x)=e_H\}$
  • The image $Im(f)$ is defined as $\{f(x)|x\in G\}\subseteq H$
• If $f$ is bijective, it is called a group isomorphism and we denote $G\cong H$
• The quotient group $G/H=\{xH|x\in G\}$ with $xH\cdot yH=(xy)H$ is a group and the quotient map $q:G\to G/H$ given by $x\mapsto xH$ is a group homomorphism
• Cyclic groups:
  • For a group $G$ and element $g\in G$, the order of $g$ $o(g)$ is the minimal natural number $n$ such that $g^n=e$. If no such number exists, we set $o(g)=\infty$.
  • Cauchy’s theorem: For a finite abelian group $G$ and prime $p$, if $p\mid \#G$, there exists an element $g\in G$ with $o(g)=p$
    • (partial converse of Lagrange’s theorem)
  • A group $G$ is called cyclic if there exists an element $g\in G$ such that *the group generated by $g$, $⟨g⟩:=\{g^n\mid n\in \mathbb{Z}\}$, equals $G$
  • Any cyclic group is abelian and isomorphic to ${\mathbb{Z}}_{\#G}$ (because any element can be expressed uniquely as $g^i$ for $i\in {\mathbb{Z}}_{\#G}$)
  • Euler totient function: $\phi (n)=\#\{k\mid 1\le k\le n\wedge \gcd (n,k)=1\}$
  • An element in $k\in {\mathbb{Z}}_n$ is a generator if $gcd(k,n)=1$, and $\phi (n)$ gives the number of generators of ${\mathbb{Z}}_n$
  • Fundamental Theorem of Cyclic Groups: For a cyclic group $G$
    • Any subgroup is cyclic
    • For any $k\mid \#G$, $⟨g^{\#G/k}⟩$ is the unique subgroup of size $k$
  • Lagrange’s theorem implies that any prime-order group is cyclic!

Fields

• A field is a set $\mathbb{F}$ with binary operations $+:\mathbb{F}\times \mathbb{F}\to \mathbb{F}$ and $\cdot :\mathbb{F}\times \mathbb{F}\to \mathbb{F}$ and elements $0\ne 1\in \mathbb{F}$ such that:
  • Both $(\mathbb{F},+,0)$ and $(\mathbb{F}\setminus \{0\},\cdot ,1)$ are abelian groups
  • For every $x,y,z\in \mathbb{F},x\cdot (y+z)=x\cdot y+x\cdot z$
• The field characteristic is the minimal number $n$ such that $1$ added to itself $n$ times is $0$ (or $0$, if no such number exists)
• A subfield needs to contain $0$ and $1$ and be closed under the two operations.
• Polynomials over a field:
  • Polynomial in one variable: a formal expression of the form $f(x)={\sum }_{i=0}^n{a}_i\cdot x^i$ where $a_i\in \mathbb{F}$ are the coefficients, the terms $a_i\cdot x^i$ are called monomials, $\mathrm{deg}f:=n$ is the degree and the set of all polynomials is denoted as $\mathbb{F}[x]$.
  • Polynomials can be added, subtracted, multiplied and divided. Division example:
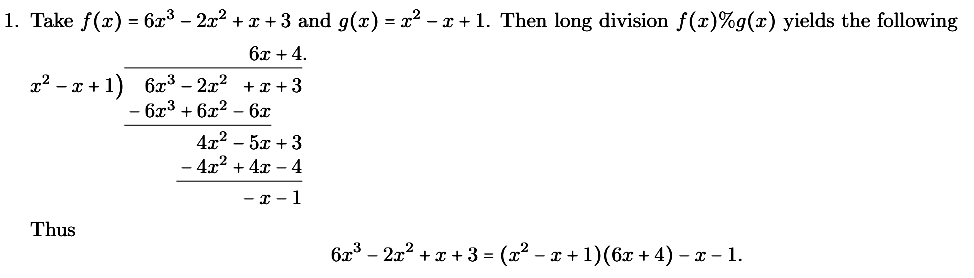
  • ⇒ Polynomials form a ring: It’s like a field, but not all polynomials have multiplicative inverses
  • A polynomial as a root $\alpha$ iff. it is divisible by $(x-\alpha )$
    • ⇒ a polynomial can have at most $n$ roots
  • A prime (or irreducible) polynomial is one that cannot be expressed as a product of two non-constant polynomials.
  • Monic polynomial: Leading coefficient is 1.
• Modulo algorithmic of polynomials: For a prime polynomial $\varphi$ over a field $\mathbb{F}$, we can define a field ${\mathbb{F}}_{\varphi (x)}=\mathbb{F}[x]/(\varphi )$ ⇒ $\varphi$ does not have a root in $\mathbb{F}$, but in ${\mathbb{F}}_{\varphi (x)}$ it has a root: $x$
• A splitting field for a polynomial $f$ is one where $f$ can be expressed as a product of linear factors which is minimal, i.e., there is no subfield with the same property.
  • It always exists: we can just repeat extending the field by non-linear prime polynomials until we have none left.
  • If $\mathbb{F}$ is a finite field of size $q=p^n$ (for a prime $p$ and some natural number $n$), it is a splitting field of $x^q-x$
• Galois fields: For any prime $p$ and natural number $n$, there exists a finite field of size $p^n$. Conversely, any finite field has a size of the form $p^n$, and all fields of the same size are isomorphic. Therefore, all finite fields can be denoted as $GF(p^n)$.
• Algebraic Closure: For a finite field $\mathbb{F}={\mathbb{F}}_q$ for $q=p^m$, the algebraic closure $\overline{\mathbb{F}}={\bigcup }_{n\in \mathbb{N}}{\mathbb{F}}_{q^n}$ is a infinite-size field with characteristic $q$ where all polynomials split.
  • To add or multiply two elements from ${\mathbb{F}}_{n_1}$ and ${\mathbb{F}}_{n_2}$, embed them into ${\mathbb{F}}_{n_1\cdot n_2}$ and do the operation there
• The $n$th roots of unity ${\mu }_n$ on a prime field ${\mathbb{F}}_p$ is the sets of roots of $x^n-1$ in ${\overline{\mathbb{F}}}_p$
  • If $p$ does not divide $n$, ${\mu }_n$ is a cyclic group
• Lagrange interpolation: Given points $(x_0,y_0),...(x_n,y_n)\in \mathbb{F}\times \mathbb{F}$, the ith Lagrange polynomial is $L_i(x):=\frac{{\prod }_{j\ne i}x-x_j}{{\prod }_{j\ne i}{x}_i-x_j}$ and the Lagrange interpolation of the points is $L(x):={\sum }_{i=0}^n{y}_i\cdot L_i(x)$
• Fast Fourier Transform (FFT):
  • Polynomials can be represented in evaluation form (“sampling”) and coefficient form (“vector”)
  • The FFT is an efficient algorithm to compute the Discrete Fourier Transform (DFT), which is a matrix-vector product of the Vandermonde matrix with the polynomial’s coefficients ⇒ performs evaluation:
  • For efficiency, we choose $x=w$, where $w$ is an $n$th root of unity
  • Algorithm below
  • The inverse of $FF{T}_w$ is $\frac{1}{n}FF{T}_{w^{-1}}$ FFT Algorithm:

def fft(f, omega):
    # Base case
    n = len(f)
    if n == 1:
        return f  # Nothing to transform if there's only 1 data point
 
    # Separate even and odd-indexed elements
    f_E = [f[2*i] for i in range(n//2)]
    f_O = [f[2*i + 1] for i in range(n//2)]
 
    # Recursively compute FFT on halves, using omega^2 as (n/2)-th root of unity
    F_E = fft(f_E, omega * omega)
    F_O = fft(f_O, omega * omega)
 
    # Combine step: allocate output and perform the butterfly merges
    F = [0] * n
    for j in range(n//2):
        t = (omega ** j) * F_O[j]
        F[j] = F_E[j] + t
        F[j + n//2] = F_E[j] - t
 
    return F

More resources:

• https://darkrenaissance.github.io/darkfi/crypto/fft.html
• https://codeberg.org/darkrenaissance/darkfi/src/branch/master/script/research/zk/fft

Vector Spaces

• A vector space $V$ over a field $\mathbb{F}$ is a set $V$ with a distinguished element $0_V\in V$ and binary operations $+:V\times V\to V$ and $\cdot :\mathbb{F}\times V\to V$ such that:
  • $(V,+,0)$ is an abelian group
  • Scalar multiplication is associative and distributive
• A subspace is a subset of a vector space that is closed under the two operations
• A linear map between to vector spaces $V,W$ (over the same field) is a function $f:V\to W$ such that:
  • $f(av)=a\cdot f(v)$
  • $f(v+v^{\prime })=f(v)+f(v^{\prime })$
• A basis of a finite vector space is an ordered set of linearly independent vector space elements which span the entire vector space. All bases have the same number of elements which is called the dimension of the vector space.
  • ⇒ Any finite vector space for dimension $n$ is isomorphic to ${\mathbb{F}}^n$, representing each element as a linear combination of its basis vectors.

Projective Coordinates

• The projective line ${\mathbb{P}}_{\mathbb{K}}^1$ over a field $\mathbb{K}$ is the quotient set of the punctured affine plane $\mathbb{K}\times \mathbb{K}\setminus \{(0,0\}$ by the equivalence relation $\forall \lambda \in \mathbb{K}\setminus \{0\}(x,y)\sim \lambda (x,y)$
• The projective plane is defined as ${\mathbb{P}}_{\mathbb{K}}^2={\mathbb{K}}^3\setminus \{(0,0,0)\}/\sim$
• The equivalence class of a point $(x,y,z)$ is denoted by $(x:y:z)$
• …

Reed-Solomon error-correcting codes

• Alphabet: Finite set $\Sigma$ of size $q$
• Hamming distance of two strings $x,y\in {\Sigma }^n$: $\Delta (x,y)=|\{i\in [n]:x_i\ne y_i\}|$
• $(n,k,d)$ code: Functions $E:{\Sigma }^k\to {\Sigma }^n,D:{\Sigma }^n\to {\Sigma }^k$ such that for all $u\in {\Sigma }^k,w\in {\Sigma }^n$ with $\Delta (E(u),w)\le e$, we have $D(w)=u$
  • Rate: $R=k/n$
  • Relative distance: $\delta =d/n$
• Singleton bound: For any code, $R+\delta \le 1+1/n$
• Maximum distance separable (MDS) code: A code that meets the singleton bound with equality
• A linear code $\mathcal{C}$ is a code that is a $k$-dimensional subspace of ${\mathbb{F}}_q^n$
  • $⟹$ $\Delta$ satisfies the triangle equality

Errors?

• Example 5.15: How can 2 times 2 be 0? Then $(\mathbb{F}\setminus 0,\cdot ,1)$ would not be a group?
• Example 5.60: The factor should be $(x^2+\sqrt{2})$?
• Misspelling of “Fanu plane”